We all (OK not all, just the geeks among us) remember how excited we were in 2015, when the date March 14 became 3/14/15, which is the first five digits of π (the ratio of a circle’s diameter to its circumference, among other things). Pi day! We had chicken pie for dinner ¹ and apple pie for dessert!

As cool as pi day was, 2018 will bring us two such excellent days: φ day and e day! ²

Φ (Phi) day, 1/6/18

Φ (phi, pronounced fye) is also known as the golden ratio. It is this:

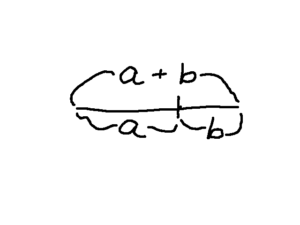
The ratio of the whole line segment (a+b) to the longer segment (a) is the same as the ratio of the longer segment (a) to the shorter segment (b).  In other words, \( \frac{a+b}{a}=\frac{a}{b}\).  If we were to call the whole thing (a+b) =1, then this means that \(\frac{1}{a}=\frac{a}{1-a}\).

Or another way to say this: φ is that number that is one more than its reciprocal.

Φ is found all over the place: in nature ³, in art, and of course in math. There are a lot of unfounded claims about φ, but there is no denying it is a very significant number. So what is this number? How can we calculate it? Start with the definition we just used, that it is one more than its reciprocal, ie\(\begin{align*}\frac{1}{a}=a-1\end{align*}\)

If we rearrange this, we get: \(\begin{align*}a^2-a-1=0\end{align*}\)

Well, that is an old friend: a quadratic equation! And since we remember the formula from Algebra 2:\(\begin{align*}\frac{-b \pm \sqrt{ b^2-4ac}}{2a}\end{align*}\) for \(\begin{align*}ax^2+bx+c=0\end{align*}\)

we can just plug the values in, and we get (taking just the positive-number solution): \(\begin{align*}\frac{1+\sqrt{5}}{2}\end{align*}\). Pull out your calculators (tip: your iPhone calculator will be a scientific calculator if you turn it sideways, so you can do square roots), take the square root of 5, add 1, divide by 2. You get 1.618033988749… . This is the Golden Ratio! And this is why 1/6/18 is Phi Day!

e day, 2/7/18

As wonderful as φ is, e ⁴ is a far more important and significant number in math. Like φ, e is an irrational number; that is, it cannot be expressed as the ratio of whole numbers, and in decimal form, it continues infinitely without repeating. ⁵

Rather than give a mathematical explanation for e, let’s just use an example: compounding interest. ⁶

Let’s say you have $100, and you invest it such that you get 100% interest after a year. So a year from today, you get $100 interest, and you now have $200. Sign me up.

But how about if we compound that interest semi-annually, ie you get 50% after 6 months, and another 50% at the end of the year. So in 6 months you get $50 interest, and you now have $150. At the end of the year, you get 50% interest on the $150, so you get another $75 interest. Now you have $225 at the end of the year: the magic of compound interest!

Now let’s compound the interest 10 times a year (OK in real life, it would be monthly, but the arithmetic is easier this way). It turns out you will have $259.37 (rounded off) at the end of the year. Yes!

What if you could compound the interest every day? Every second? Every microsecond? Continuously? Is there a limit to how much you will earn? Yes there is! The upper limit, if you compound continuously, is that you will have $271.82 (rounded off) at the end of the year. This, my friends, is e: 2.718281828459…(irrational, so continues infinitely).

And that is why 2/7/18 is e day!

1. courtesy of Mike DeEmedio
2. None of this is as complicated as it looks at first glance.
3. https://www.youtube.com/watch?v=ahXIMUkSXX0, a short video by the incomparable Vi Hart; be sure to watch Parts 1, 2 and 3, and you will understand why the leaves of a plant express the Golden Ratio!
4. Named for Leonhard Euler (pronounced “oiler”), the greatest mathematician of the 18th century, who probably should have had an NFL team, from Houston maybe, named after him
5.  π is also an irrational number, which may prompt the question: how many irrational numbers are there? Weirdly, although the whole numbers, and the rational numbers, are infinite in number, the irrational numbers are even more infinite! Yes, this will be a future post.
6.  e turns up in pure math, geometry, number theory, engineering, you name it. This is just a trivial example